4.10.2017
In the last article on Qt parallel programming, I showed a simple example how large amounts of jpg images can be scalled down in parallel.
The most difficult thing when writing articles like this is to invent some meaningful examples. Scaling down images in previous article is impractical example because my PC did not even spin up fans on CPU. Acceleration by three seconds is not the result, for which I would like to learn parallel programming.
As another example, I have invented the task much more practical and requiring much more computational power - calculation ot the π number using the Monte Carlo method.
Metoda Monte Carlo na Wikipedii
The Monte Carlo method is one of the simulation computational practices. It can be used in applications typically in two different cases:
Calculation of the π number by Monte Carlo method is the first case - the developer implementing the calculation does not know how to calculate the π number, but he can very easily decide if some point lies inside the circle or outside the circle.
If you want to calculate the π number using Monte Carlo method, you even does not need a computer. You need only a paper, a ruler, a compass, a handful of poppies, and a lot of patience in grain counting.
On a paper with a circle and a square drawn, poppy pop and count as many poppy grains the fell into a square and how many grains fell into the circle. The ratio of the number of grains can then be easily converted to the π number. The whole process can of course be much less effortless and with more accuracy implemented on your computer.
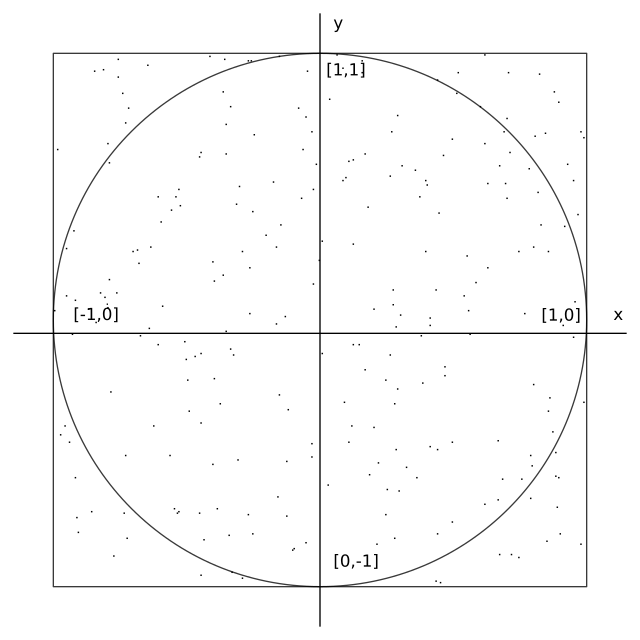
Equation of the Circle with radius 1 and the center in [0,0] is
x² + y² = 1
For every random point with coordinates [x,y] we can decide, if the point lies inside or outside of the circle. For every point two different cases can occur:
x² + y² <= 1 // the point lies inside the circle
or
x² + y² > 1 // the point lies outside the circle
The area of the circle is calculated as:
Scircel = π r²
For the circle with radius 1 we can write:
Scircle = π
On the image is circle inscribed in a square of the side 2 and an area 4. The area is calculated as:
Ssquare = (2r)² = 2² = 4
The ratio of the square area and the circle area is:
x = Scircle / Ssquare = 4 / π
then
π = 4 / x
Some randomly generated points in the inverval from [-1,-1] to [1,1] lies inside the circle, but all poins lies inside the square. For the π number calculation we have to generate number of random points and count the number of points inside the circle. Then we can calculate the π number from their ratio. The algorithm can be simplified if we generate random number in the inverval from [0,0] to [1,1]. Then the π number can be calculated as:
π = 4 * Ncircle / Nsquare
Of course, the result is only approximate and its usability strongly depends on the quality of the random number generator and the number of points.
Input data could be randomly generated points. But such a naive approach has two cons:
It looks that the input data are not needed. But the parallel processing must be driven by input data. This can be accomplished by a simple QList, whose values are simply ignored. Just make QList big enough. Because I do not know how to do QList large enough directly, I made a simple loop to generage input values:
QList<double> data = QList<double>() << 0;
for (int i=0; i<10; i++) {
data += data;
}
The calculation function generates random x and y and determine if the point lies inside circle. The whole procedure is repeated in the loop and after a sufficient number of repetitions (here 16384) of the cycles returns the ratio of the number of points generated and the number of points inside a circle. This ratio should be close to the number π. Please, note that the function returns the result - we will work with the result in the next step.
double pi(int) {
const int count = 16384;
int incircle = 0;
for (int i=0; i<count; i++) {
double x=((double)rand()/(double)RAND_MAX);
double y=((double)rand()/(double)RAND_MAX);
if (x*x + y*y <= 1) {
incircle += 1;
}
}
return ((double)incircle) / ((double)count);
}
Once the map function processed over the entire input set of data, we get the list different suggestions, how the number π might look like. Each calculated value will vary. Average the calculated values is the task of the reduction function. It is a bit indirect - the reduction function counts only the sum of all suggestions, for the correct result it is necessary to divide the sum by the number of input data after the reduction.
void sum(double& sum, const double& pi) {
sum += pi;
}
double sumpi = QtConcurrent::blockingFilteredReduced (
data, // Input data
pi, // Map function
sum // Reduce function
);
double pi = 4.0 * sumpi / ((double)data.size());
#include <QtConcurrent>
#include <QDebug>
double pi(double) {
const int count = 16384;
int incircle = 0;
for (int i=0; i<count; i++) {
double x=((double)rand()/(double)RAND_MAX);
double y=((double)rand()/(double)RAND_MAX);
if (x*x + y*y <= 1) {
incircle += 1;
}
}
return ((double)incircle) / ((double)count) ;
}
void sum(double& sum, const double& pi) {
sum += pi;
}
int main(int argc, char **argv) {
QCoreApplication app(argc, argv);
QList<double> data = QList<double>() << 0.0;
for (int i=0; i<10; i++) {
data += data;
}
double sumpi = QtConcurrent::blockingMappedReduced (data, pi, sum);
double pi = 4.0 * sumpi / ((double)data.size());
qDebug() << pi;
}
This time I did not create the single-thread version. The application performs only mathematical computations in CPU, it should be sufficient to compare CPU time consumed and real run time:
time ./pi 3.14131 real 0m10.001s user 0m13.769s sys 1m0.080s
Total CPU time is 73.849s, which correspons with CPU cores number (8 cores). It is amazing that the AMD FX-8350 CPU can handle the CPU cores perfectly in this type of task. The eight cores in the CPU have only four FPU computing units. Each pair of cores is in the same position as the two pupils sitting in one bench, sharing one calculator.
Please, notice the system time consumed. I think that the random number generator spent most of system time. This is also one of the reasons why you need to move random numbers to parallel calculations. Random number are generated by about 6/7 of the CPU time. It probably causes such a great acceleration despite that the processor has only four FPUs - most machine time has been consumed in integer calculations so the FPUs were not shared by the CPU cores.
3.14131 3.142 3.14162 3.14176 3.14185 3.14148 3.14209
It is obvious that the Monte Carlo method gives only approximate results. But this simple method can find the value of the π number with approximately the same accuracy as the average engineer has in his head.
The importance of the Monte Carlo method is not accuracy but the fact, that it can provide approximate results in situations where another method is difficult, unreal or unknown.
This article is one of several articles on parallel programming in Qt. Watch this site, watch our Twitter. Further parts will follow.